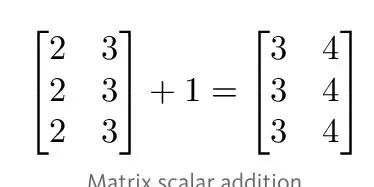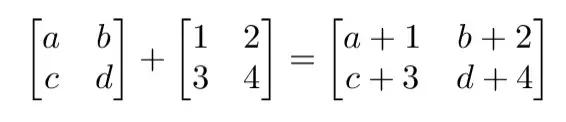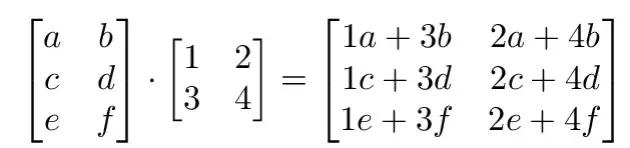| 数加 | 数乘/积 | 互相加 | 互相乘/点积 | |
| 数学向量 |
标量运算即为向量和数字间的运算。向量与数的运算就是向量内每一个元素与这一个数进行相应的运算。如下图的一个标量运算:
|
一个数乘以一个向量等于这个数同向量中的每个元素相乘 2 [1 2 3] = [2 4 6] |
2个向量对应位置的元素相加 [1 2 3] + [1 2 3] = [2 4 6] |
一个行向量乘以一个列向量,是两个向量对位相乘再相加,结果是一个实数.
|1 2 3 | * |
| 数学矩阵 |
矩阵的标量运算矩阵的标量运算和向量的标量运算是一样的。可以简单地将标量和矩阵中的每一个元素做运算处理(如加、减、乘、除等)。 同向量
|
同向量 |
矩阵间的运算为了能进行加减运算,两个矩阵的阶必须相等。然后我们可以对两个矩阵相应的元素进行运算处理。如下图就是两阶方阵的加法。
|
m×n 阶矩阵左乘 n×k 阶矩阵的结果是 m×k 阶矩阵 矩阵乘法的步骤和向量点积的过程是相似的,它们都是由对应位置的元素进行乘积并相加而得出
|
| python列表 | 不能操作 |
重复列表 ['a','b'] * 2 结果为 ['a', 'b', 'a', 'b'] |
列表拼接 ['a','b'] + [1, 2] 结果为 ['a', 'b', 1, 2] |
不能操作 |
| np.array | 同数学矩阵 | 同数学矩阵 | 同数学矩阵 | 见以下例子,np.multiply()和np.dot() |
| np.matrix | 同数学矩阵 | 同数学矩阵 | 同数学矩阵 | 见以下例子,np.multiply()和np.dot() |
在 numpy 中,如果向量是一维的,那么他就能看作是一个标量,与其他多维向量的运算就相当于一个数。
向量相乘 称为 点积
下面通过python代码说明上面的 np.array及np.matrix
1 np.multiply()函数
功能:数组或矩阵的对应位置元素相乘。
A = np.array([[0,1],[2,3]])
B = np.array([[1,2],[3,4]])
print(np.multiply(A, B)) # 数组对应位置元素相乘
array([[0, 2],
[6, 12]])
2 np.dot() 函数
功能:执行数学中的矩阵乘法运算。即 m×n 阶矩阵左乘 n×k 阶矩阵的结果是 m×k 阶矩阵
A = np.array([[0,1],[2,3]])
B = np.array([[1,2],[3,4]])
print(np.dot(A, B)) # 执行矩阵乘法运算
array([[3, 4],
[11, 16]])


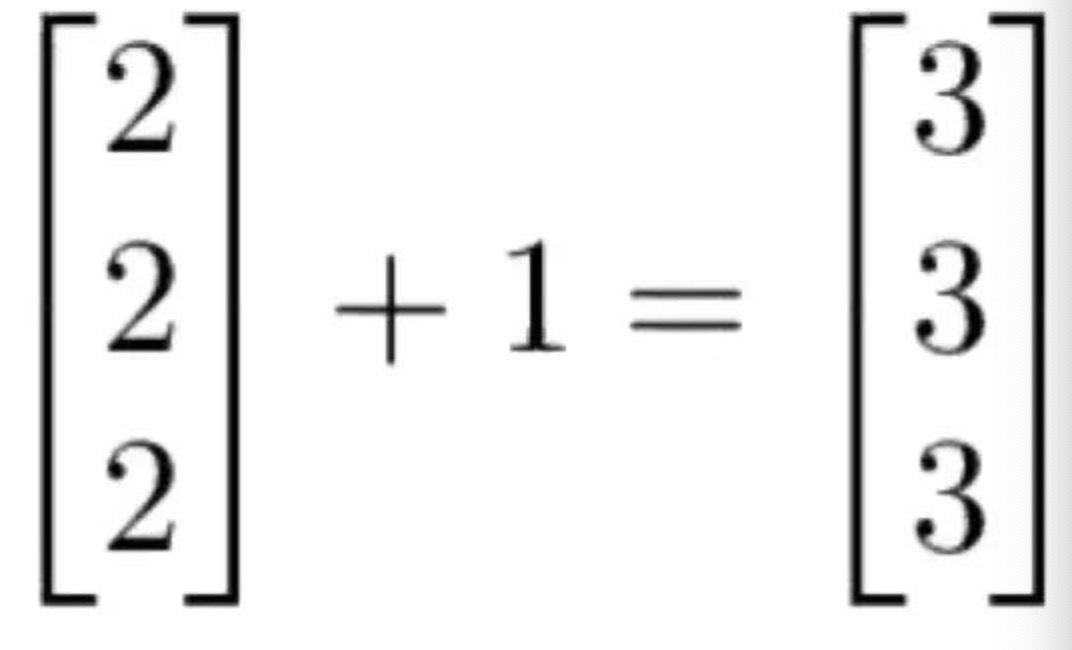
 = 1*1 + 2*2 + 3*3 = 14
= 1*1 + 2*2 + 3*3 = 14